This tutorial demonstrates how to connect a couple of different equation systems to one larger equation for an application in chemical engineering. Here, we have three equation systems for condenser, tray, and reboiler. This example is relatively complex as it features optional elements, such as parameter lists, functions, and connectors. Our goal is to simulate the distillation of water (component 1) and methanol (component 2).
Model description
In the following, we introduce the model of the three sub-systems. Afterwards, we show the functions calculating the thermodynamic properties liquid molar enthalpy, vapor pressure, and enthalpy of vaporization.
Condenser
The condenser model consists of the component balances, the equilibrium (we assume a thermodynamically ideal system), the summation relations for liquid and vapor phase, the energy balance, the momentum balance, the reflux ratio, and the mixing rule for the liquid enthalpy:
![Rendered by QuickLaTeX.com \begin{align*}&0 = F^{V,\mathrm{in}} \cdot y_c^\mathrm{in} - \left( F_\mathrm{reflux}^L + D\right) \cdot x_{\mathrm{C},c} \\[2ex]&y_{\mathrm{C},c} \cdot P_\mathrm{C} = x_{\mathrm{C},c} \cdot P_{\mathrm{C},c}^{LV} \\[2ex]&1 = \sum_{c=1}^{NC} x_{\mathrm{C},c} \\[2ex]&1 = \sum_{c=1}^{NC} y_{\mathrm{C},c} \\[2ex]&0 = Q_\mathrm{C} + F^{V,\mathrm{in}} h^{V,\mathrm{in}} - \left(F_\mathrm{reflux}^L + D\right) \cdot h_\mathrm{C}^L \\[2ex]&\Delta P = P_{tr=NTR} - P_\mathrm{C} \\[2ex]&F_\mathrm{reflux}^L = r \cdot D \\[2ex]&h_\mathrm{C}^L = \sum_{c=1}^{NC} x_{\mathrm{C},c} \cdot h_{\mathrm{C},c}^L.\end{align*}](https://mosaic-modeling.de/wp-content/ql-cache/quicklatex.com-eb92064271f18191112245924f38defe_l3.png)
Trays
The tray model consists of similar equations. In addition, we have the mixing rule for the feed enthalpy, the liquid enthalpy, and the vapor enthalpy. The latter is calculated as sum of liquid enthalpy and enthalpy of vaporization:
![Rendered by QuickLaTeX.com \begin{align*}&0 = F_{tr}^{\mathrm{f},L} \cdot x_c^\mathrm{f} + F_{tr+1}^L \cdot x_{tr+1,c} + F_{tr-1}^V \cdot y_{tr-1,c} - F_{tr}^L \cdot x_{tr,c} - F_{tr}^V \cdot y_{tr,c} \\[2ex]&y_{tr,c} \cdot P_{tr} = x_{tr,c} \cdot P_{tr,c}^{LV} \\[2ex]&1 = \sum_{c=1}^{NC} x_{tr,c} \\[2ex]&1 = \sum_{c=1}^{NC} y_{tr,c} \\[2ex]&0 = F_{tr}^{\mathrm{f},L} \cdot h^{\mathrm{f},L} + F_{tr+1}^L \cdot h_{tr+1}^L + F_{tr-1}^V \cdot h_{tr-1}^V - F_{tr}^L \cdot h_{tr}^L - F_{tr}^V \cdot h_{tr}^V \\[2ex]&\Delta P = P_{tr-1} - P_{tr} \\[2ex]&h^{\mathrm{f},L} = \sum_{c=1}^{NC} x_c^\mathrm{f} \cdot h_c^{\mathrm{f},L} \\[2ex]&h_{tr}^L = \sum_{c=1}^{NC} x_{tr,c} \cdot h_{tr,c}^L \\[2ex]&h_{tr}^V = \sum_{c=1}^{NC} y_{tr,c} \cdot \left(h_{tr,c}^L + \Delta h_{tr,c}^{LV}\right).\end{align*}](https://mosaic-modeling.de/wp-content/ql-cache/quicklatex.com-9470e10681fcd68267012685c55f4cb8_l3.png)
Reboiler
The reboiler equations also consist of component balances, thermodynamic equilibrium, summation terms, energy balance, and mixing rules for liquid and vapor enthalpy:
![Rendered by QuickLaTeX.com \begin{align*}&0 = F_\mathrm{R}^{L,\mathrm{in}} \cdot x_{\mathrm{R},c}^\mathrm{in} - B \cdot x_{\mathrm{R},c} - F_\mathrm{R}^V \cdot y_{\mathrm{R},c} \\[2ex]&y_{\mathrm{R},c} \cdot P_\mathrm{R} = x_{\mathrm{R},c} \cdot P_{\mathrm{R},c}^{LV} \\[2ex]&1 = \sum_{c=1}^{NC} x_{\mathrm{R},c} \\[2ex]&1 = \sum_{c=1}^{NC} y_{\mathrm{R},c} \\[2ex]&0 = Q_\mathrm{R} + F_\mathrm{R}^{L,\mathrm{in}} \cdot h_\mathrm{R}^{L,\mathrm{in}} - B \cdot h_\mathrm{R}^L - F_\mathrm{R}^V \cdot h_\mathrm{R}^V \\[2ex]&h_\mathrm{R}^L = \sum_{c=1}^{NC} x_{\mathrm{R},c} \cdot h_{\mathrm{R},c}^L \\[2ex]&h_\mathrm{R}^V = \sum_{c=1}^{NC} y_{\mathrm{R},c} \cdot \left(h_{\mathrm{R},c}^L + \Delta h_{\mathrm{R},c}^{LV}\right).\end{align*}](https://mosaic-modeling.de/wp-content/ql-cache/quicklatex.com-67d60b0e816a8d34bbc7233092edd1ab_l3.png)
Functions
Finally, the liquid enthalpy, the vapor pressure, and the enthalpy of vaporization are calculated using DIPPR equations (100, 101, and 106):
![Rendered by QuickLaTeX.com \begin{align*}&h^L (T) = A_{d100} \cdot (T-T^{h,ref}) + \frac{B_{d100}}{2} \cdot ((T)^{2}-(T^{h,ref})^{2}) + \frac{C_{d100}}{3} \cdot ((T)^{3}-(T^{h,ref})^{3}) + \frac{D_{d100}}{4} \cdot ((T)^{4}-(T^{h,ref})^{4}) + \frac{E_{d100}}{5} \cdot ((T)^{5}-(T^{h,ref})^{5}) + h^{L,ref} \\[2ex]&P^{LV} (T) = \exp(A_{d101} + \frac{B_{d101}}{T}+C_{d101} \cdot \ln(T) + D_{d101} \cdot (T)^{E_{d101}}) \\[2ex]&\Delta h^{LV} (T) = A_{d106} \cdot (1 - \frac{T}{T^{LV,ref}})^{B_{d106} + C_{d106} \cdot \frac{T}{T^{LV,ref}} + D_{d106} \cdot (\frac{T}{T^{LV,ref}})^{2} + E_{d106} \cdot (\frac{T}{T^{LV,ref}})^{3}}.\end{align*}](https://mosaic-modeling.de/wp-content/ql-cache/quicklatex.com-24f6a10d848d10af32a0966b8c650655_l3.png)
Modeling workflow
In the following, we show the workflow for setting up the equation system with two different naming policies for the variables, i.e., integrate and encapsulate. We start by defining the notation for this example. For the sake of simplicity, we limit ourselves to one notation, but the example would also work with a different notation for each unit.
Notation
Set up a notation with the following base names and indices:
Base names
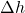 , enthalpy difference in kJ/mol
, enthalpy difference in kJ/mol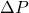 , pressure drop in bar
, pressure drop in bar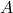 , parameter
, parameter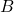 , bottom product flow in mol/s and parameter
, bottom product flow in mol/s and parameter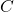 , parameter
, parameter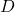 , distillate flow in mol/s and parameter
, distillate flow in mol/s and parameter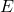 , parameter
, parameter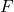 , parameter
, parameter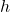 , molar enthalpy in kJ/mol
, molar enthalpy in kJ/mol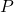 , pressure in bar
, pressure in bar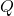 , heat flow in kW
, heat flow in kW , reflux ratio
, reflux ratio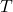 , temperature in K
, temperature in K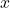 , liquid mole fraction in mol/mol
, liquid mole fraction in mol/mol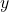 , vapor mole fraction in mol/mol
, vapor mole fraction in mol/mol
Superscripts
- f, feed
- h, enthalpy
- in, inlet
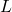 , liquid
, liquid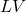 , equilibrium between liquid and vapor
, equilibrium between liquid and vapor- ref, reference
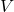 , vapor
, vapor
Subscripts
- C, condenser
- d100, DIPPR 100
- d101, DIPPR 101
- d106, DIPPR 106
- product, product
- R, reboiler
- reflux, reflux
Indices
 , component index 1…NC
, component index 1…NC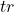 , tray index 1…NTR
, tray index 1…NTR
The resulting notation has ID 185711.
Parameter list
Go to the parameter list section and add the parameters for the DIPPR equations to the parameter list:
DIPPR 100
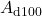 ,
, 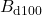 ,
, 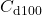 ,
, 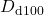 ,
,  ,
, 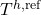 , and
, and 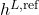
DIPPR 101
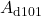 ,
, 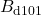 ,
, 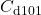 ,
, 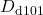 , and
, and 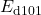
DIPPR 106
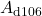 ,
, 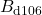 ,
, 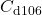 ,
, 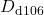 ,
, 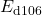 , and
, and 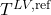
Save the parameter lists. The parameter list of this example has ID 185740.
Equations
Go to the Equation tab and perform the following steps:
- Load the notation set up above
- Enter the equations of condenser, trays, and reboiler and save them
The condenser equations have IDs 185724, 185725, 185726, 185727, 185728, 185752, 185729, and 185730.
The tray equations have IDs 185712, 185714, 185715, 185716, 185717, 185718, 185719, 185720, and 185721.
The reboiler equations have IDs 185733, 185734, 185735, 185736, 185737, 185738, and 185739.
Functions
Go to the function tab and do as follows:
- Load the notation and the parameter list set up above
- Add a reasonable description
- Go to the Interface & Body Settings and make sure that Free interface and Specify formula are selected
- Add
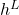 as output and
as output and 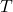 as input
as input - Add the DIPPR 100 equation as Body Specification
- Save the function
- Repeat the steps 1-6 for DIPPR 101 and DIPPR 106 with the outputs
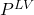 and
and 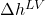 and the input
and the input 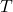 in both cases, respectively
in both cases, respectively
The functions have IDs 185741, 185742, and 185743.
Connectors
We could now solve the three systems one by one. However, we cannot connect them as, for example, the liquid flow from the condenser is ![]() , whereas the tray model expects the flow
, whereas the tray model expects the flow ![]() . Hence, we need two connectors that translate these variable names. For this purpose, go to the Connector tab and do the following:
. Hence, we need two connectors that translate these variable names. For this purpose, go to the Connector tab and do the following:
- Add a helpful description for the connector
- Activate the tab Edit Matching and select the notation of this example as both Sub and Super Notation
- Generate the missing variables for the Sub Notation and the Super Notation, i.e.,
- Sub Notation:
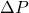 ,
, 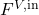 ,
, 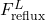 ,
, 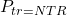 ,
, 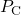 ,
, 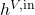 ,
, 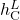 ,
, 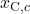 , and
, and 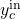
- Super Notation:
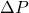 ,
, 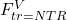 ,
, 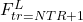 ,
, 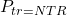 ,
, 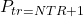 ,
, 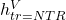 ,
, 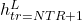 ,
, 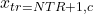 , and
, and 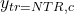
- Sub Notation:
- Select the analogous variables and click on Match to achieve the following matching:
- Make sure that the indices were matched by clicking on variable pairs that contain the index

- Save the connector for the connection of condenser and trays
- Repeat the steps 1-6 for a second reactor connecting reboiler and trays.
- Therefore, set up the the following variables in sub and super notation:
- Sub Notation:
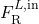 ,
, 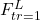 ,
, 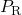 ,
, 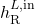 ,
, 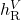 ,
, 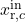 , and
, and 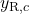
- Super Notation:
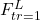 ,
, 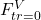 ,
, 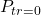 ,
, 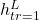 ,
, 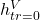 ,
, 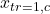 , and
, and 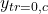
- Sub Notation:
- Match these variables as follows:
- Therefore, set up the the following variables in sub and super notation:
The connectors are available with IDs 185748 and 185750.
Equation systems
To construct the equation systems, go to the Equation System tab and take the following steps.
Condenser system
- Load the notation and add a reasonable description
- Click on “Add EQU/EQS” and add the equations for the condenser
- Make sure that the Naming policy is integrate
- Go to the tab Functions and add the DIPPR 100 function with the applied output variable
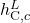 and the input
and the input 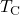
- Make sure that the applied parameter names are
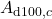 ,
, 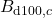 ,
, 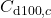 ,
, 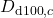 ,
, 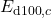 ,
, 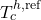 , and
, and 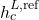
- Confirm, then add the DIPPR 101 function with the applied output variable
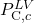 and the input
and the input 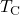
- Make that the applied parameter names are
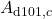 ,
, 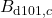 ,
, 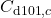 ,
, 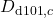 , and
, and 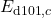
- Save the equation system
Tray system
- Load the notation and add a reasonable description
- Click on “Add EQU/EQS” and add the equations for the trays
- Make sure that the Naming policy is integrate
- Go to the tab Functions and add the DIPPR 100 function with the applied output variables
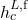 and
and 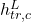 , and the inputs
, and the inputs 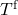 and
and 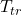 , respectively
, respectively - Make that the applied parameter names are
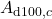 ,
, 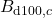 ,
, 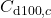 ,
, 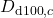 ,
, 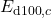 ,
, 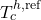 , and
, and 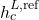
- Confirm, then add the DIPPR 101 function with the applied output variable
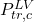 and the input
and the input 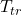
- Make that the applied parameter names are
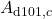 ,
, 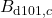 ,
, 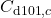 ,
, 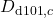 , and
, and 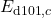
- Confirm, then add the DIPPR 106 function with the applied output variable
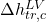 and the input
and the input 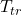
- Make that the applied parameter names are
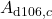 ,
, 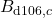 ,
, 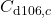 ,
, 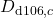 , and
, and 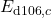 , and
, and 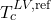
- Save the equation system
Reboiler system
- Load the notation and add a reasonable description
- Click on “Add EQU/EQS” and add the equations for the reboiler
- Make sure that the Naming policy is integrate
- Go to the tab Functions and add the DIPPR 100 function with the applied output variable
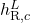 and the input
and the input 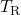
- Make that the applied parameter names are
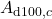 ,
, 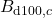 ,
, 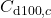 ,
, 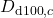 ,
, 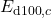 ,
, 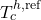 , and
, and 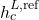
- Confirm, then add the DIPPR 101 function with the applied output variable
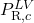 and the input
and the input 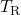
- Make that the applied parameter names are
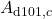 ,
, 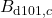 ,
, 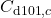 ,
, 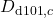 , and
, and 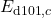
- Confirm, then add the DIPPR 106 function with the applied output variable
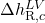 and the input
and the input 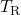
- Make that the applied parameter names are
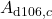 ,
, 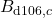 ,
, 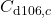 ,
, 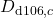 , and
, and 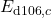 , and
, and 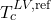
- Save the equation system
The three equation systems have the IDs 185744, 185745, and 185746.
Combined system with naming policy integrate
To combine the three sub-systems, click on “New” and do as follows:
- Load the notation and add a reasonable description
- Add the condenser sub-system with naming policy integrate, but also with the prepared connector
- Add the tray sub-system with naming policy integrate
- Add the reboiler sub-system with naming policy integrate, but also with the prepared connector
- Save the equation system
Combined system with naming policy encapsulate
To combine the three sub-systems, click on “New” and do as follows:
- Load the notation and add a reasonable description
- Add the condenser sub-system with naming policy encapsulate, but also with the prepared connector
- Add the tray sub-system with naming policy integrate
- Add the reboiler sub-system with naming policy encapsulate, but also with the prepared connector
- Save the equation system
Simulation workflow
Equation system and Indexing
Equation system and indexing for naming policy integrate
Go to the “Simulation” section and do the following:
- Load your equation system in the tab Equation System
- Set the maximum value NC to 2 and the maximum value NTR to 10 in the tab Indexing
Equation system and indexing for naming policy encapsulate
Go to the “Simulation” section and do the following:
- Load your equation system in the tab Equation System
- Set the maximum value for all NC to 2 and the maximum value for all NTR to 10 in the tab Indexing
Initialization and results
Potential problems with the naming policy integrate
As you have seen, the naming policy integrate ensures that all variables in the equation system receive the same namespace, i.e., e0. Although everything works out well here, this approach can cause problems: Imagine, you had named the temperature in the condenser and reboiler model “![]() ”. Then, these two temperatures would have received the same namespace and would be treated as the same variable. In this example, though, we have given all variables unique names so that this problem does not occur. In general, we recommend the naming policy encapsulate for such applications to avoid equal variable names by accident.
”. Then, these two temperatures would have received the same namespace and would be treated as the same variable. In this example, though, we have given all variables unique names so that this problem does not occur. In general, we recommend the naming policy encapsulate for such applications to avoid equal variable names by accident.
Variable and parameter specification for naming policy integrate
To initialize and specify the model, take the following steps:
- Initialize this example with the design values and initial guesses given in Table 1
- Save the variable specification
- Enter the parameters according to Table 2 and save the parameter specification
- Save the simulation
- Go to the Evaluation tab and generate the code for your preferred environment
- Solve the system using the generated code
This simulation is available with ID 185749 with variable specification 185751 and parameter specification 185753. The solution for all iteration variables is also given in Table 1.
Variable and parameter specification for naming policy encapsulate
If you scroll through the variables with this naming policy, you will see that three namespaces were created: e0 for the trays and those variables that are renamed by the connector, e0e0 for the condenser variables, and e0e2 for the reboiler. These names depend on the order in which the sub-systems are included in the equation system. For example, if the tray system would be loaded first, followed by condenser and reboiler system, we would have the namespaces e0, e0e1, and e0e2.
To initialize and specify the model, you could now go through all variables, reassign them as design or iteration variable, and enter their values. This takes time. You could now try instead to naively load the variable specification from above (ID 185751). However, not all variables would be matched because of the different namespaces. Instead, you can do the following:
- Click on Import Values
- Select a language specificator, e.g., Matlab NLE
- Select SpecList as Source and load the variable specification from above (ID: 185751)
- Select “Match Namespaces” and “Import Classification”
- Selecting Match Namespaces adds a second tab. Go to this tab and remove all lines by clicking on “Delete Match” at the bottom right corner
- Click on “+ Match” and enter the namespace e0
- You can now select three namespaces on the right side in the column System
- Select the namespace e0 on the right side and click on “Test Import”. You will now see which variables will be changed if you import them. Close this window and click on “Import”.
- Repeat this step by changing the namespace in the system to e0e0 (test import and then import) and e0e2 (test import and then import)
- Your whole system should now be initialized in the same way as the simulation with the naming policy integrate and have a degree of freedom equal to zero
- Save the variable specification
- Go to the parameter specification and import the parameters the same way as for the variable specification because the parameters also appear in different namespaces now
- Save the parameter specification
- Save the simulation
- Go to the Evaluation tab and generate the code for your preferred environment
- Solve the system using the generated code
This simulation is available with ID 185755 with variable specification 185756 and parameter specification 185757. The solution for all iteration variables is also given in Table 1.
| Namespace (integ./encap.) | Name | Value / Initial guess | Solution |
|---|---|---|---|
| e0 / e0 | 1.0e-4 | ||
| e0 / e0 | 0.0 | ||
| e0 / e0 | 0.0 | ||
| e0 / e0 | 0.0 | ||
| e0 / e0 | 0.0 | ||
| e0 / e0 | 1000.0 | ||
| e0 / e0 | 0.0 | ||
| e0 / e0 | 0.0 | ||
| e0 / e0 | 0.0 | ||
| e0 / e0 | 0.0 | ||
| e0 / e0 | 0.0 | ||
| e0 / e0 | 1.0 | ||
| e0 / e0e0 | 2.0 | ||
| e0 / e0e2 | 365.0 | ||
| e0 / e0 | 351.0 | ||
| e0 / e0 | 0.55 | ||
| e0 / e0 | 0.45 | ||
| e0 / e0e2 | 1000.0 | 629.22 | |
| e0 / e0e0 | 1000.0 | 370.78 | |
| e0 / e0 | 1000.0 | 1027.07 | |
| e0 / e0 | 1000.0 | 1051.67 | |
| e0 / e0 | 1000.0 | 1070.55 | |
| e0 / e0 | 1000.0 | 1080.52 | |
| e0 / e0 | 1000.0 | 1084.77 | |
| e0 / e0 | 1000.0 | 1086.98 | |
| e0 / e0 | 1000.0 | 1100.37 | |
| e0 / e0 | 1000.0 | 1107.59 | |
| e0 / e0 | 1000.0 | 1110.70 | |
| e0 / e0 | 1000.0 | 111.90 | |
| e0 / e0 | 1000.0 | 1112.34 | |
| e0 / e0 | 1000.0 | 1656.29 | |
| e0 / e0 | 1000.0 | 1680.89 | |
| e0 / e0 | 1000.0 | 1699.77 | |
| e0 / e0 | 1000.0 | 1709.74 | |
| e0 / e0 | 1000.0 | 1713.99 | |
| e0 / e0 | 1000.0 | 716.20 | |
| e0 / e0 | 1000.0 | 729.59 | |
| e0 / e0 | 1000.0 | 736.81 | |
| e0 / e0 | 1000.0 | 739.92 | |
| e0 / e0 | 1000.0 | 741.12 | |
| e0 / e0 | 1000.0 | 741.56 | |
| e0 / e0e2 | -200.0 | -231.49 | |
| e0 / e0 | -200.0 | -184.83 | |
| e0 / e0 | -200.0 | -177.11 | |
| e0 / e0 | -200.0 | -171.87 | |
| e0 / e0 | -200.0 | -169.29 | |
| e0 / e0 | -200.0 | -168.23 | |
| e0 / e0 | -200.0 | -167.82 | |
| e0 / e0 | -200.0 | -164.83 | |
| e0 / e0 | -200.0 | -163.31 | |
| e0 / e0 | -200.0 | -162.68 | |
| e0 / e0 | -200.0 | -162.43 | |
| e0 / e0 | -200.0 | -162.34 | |
| e0 / e0 | -200.0 | -226.39 | |
| e0 / e0 | -200.0 | -220.96 | |
| e0 / e0 | -200.0 | -217.17 | |
| e0 / e0 | -200.0 | -215.28 | |
| e0 / e0 | -200.0 | -214.49 | |
| e0 / e0 | -200.0 | -207.20 | |
| e0 / e0 | -200.0 | -201.98 | |
| e0 / e0 | -200.0 | -199.33 | |
| e0 / e0 | -200.0 | -198.22 | |
| e0 / e0 | -200.0 | -197.80 | |
| e0 / e0 | -200.0 | -197.64 | |
| e0 / e0 | -200.0 | -219.16 | |
| e0 / e0 | 1.0 | 1.0011 | |
| e0 / e0 | 1.0 | 1.0010 | |
| e0 / e0 | 1.0 | 1.0009 | |
| e0 / e0 | 1.0 | 1.0008 | |
| e0 / e0 | 1.0 | 1.0007 | |
| e0 / e0 | 1.0 | 1.0006 | |
| e0 / e0 | 1.0 | 1.0005 | |
| e0 / e0 | 1.0 | 1.0004 | |
| e0 / e0 | 1.0 | 1.0003 | |
| e0 / e0 | 1.0 | 1.0002 | |
| e0 / e0 | 1.0 | 1.0001 | |
| e0 / e0 | 1.0 | 1.0 | |
| e0 / e0e0 | -40000.0 | -39265.76 | |
| e0 / e0e2 | 40000.0 | 39487.86 | |
| e0 / e0e0 | 340.0 | 337.32 | |
| e0 / e0 | 340.0 | 358.42 | |
| e0 / e0 | 340.0 | 352.83 | |
| e0 / e0 | 340.0 | 349.54 | |
| e0 / e0 | 340.0 | 348.04 | |
| e0 / e0 | 340.0 | 347.44 | |
| e0 / e0 | 340.0 | 42.54 | |
| e0 / e0 | 340.0 | 339.55 | |
| e0 / e0 | 340.0 | 338.17 | |
| e0 / e0 | 340.0 | 337.61 | |
| e0 / e0 | 340.0 | 337.40 | |
| e0 / e0e2 | 0.5 | 0.87 | |
| e0 / e0e2 | 0.5 | 0.13 | |
| e0 / e0 | 0.5 | 0.74 | |
| e0 / e0 | 0.5 | 0.60 | |
| e0 / e0 | 0.5 | 0.50 | |
| e0 / e0 | 0.5 | 0.45 | |
| e0 / e0 | 0.5 | 0.43 | |
| e0 / e0 | 0.5 | 0.24 | |
| e0 / e0 | 0.5 | 0.11 | |
| e0 / e0 | 0.5 | 0.04 | |
| e0 / e0 | 0.5 | 0.02 | |
| e0 / e0 | 0.5 | 0.005 | |
| e0 / e0 | 0.5 | 0.001 | |
| e0 / e0 | 0.5 | 0.26 | |
| e0 / e0 | 0.5 | 0.4 | |
| e0 / e0 | 0.5 | 0.5 | |
| e0 / e0 | 0.5 | 0.55 | |
| e0 / e0 | 0.5 | 0.57 | |
| e0 / e0 | 0.5 | 0.76 | |
| e0 / e0 | 0.5 | 0.89 | |
| e0 / e0 | 0.5 | 0.96 | |
| e0 / e0 | 0.5 | 0.98 | |
| e0 / e0 | 0.5 | 0.995 | |
| e0 / e0 | 0.5 | 0.999 | |
| e0 / e0e0 | 0.5 | 0.0003 | |
| e0 / e0e0 | 0.5 | 0.9997 | |
| e0 / e0 | 0.5 | 0.66 | |
| e0 / e0 | 0.5 | 0.43 | |
| e0 / e0 | 0.5 | 0.28 | |
| e0 / e0 | 0.5 | 0.20 | |
| e0 / e0 | 0.5 | 0.17 | |
| e0 / e0 | 0.5 | 0.16 | |
| e0 / e0 | 0.5 | 0.07 | |
| e0 / e0 | 0.5 | 0.03 | |
| e0 / e0 | 0.5 | 0.01 | |
| e0 / e0 | 0.5 | 0.004 | |
| e0 / e0 | 0.5 | 0.001 | |
| e0 / e0 | 0.5 | 0.34 | |
| e0 / e0 | 0.5 | 0.57 | |
| e0 / e0 | 0.5 | 0.72 | |
| e0 / e0 | 0.5 | 0.80 | |
| e0 / e0 | 0.5 | 0.83 | |
| e0 / e0 | 0.5 | 0.84 | |
| e0 / e0 | 0.5 | 0.93 | |
| e0 / e0 | 0.5 | 0.97 | |
| e0 / e0 | 0.5 | 0.99 | |
| e0 / e0 | 0.5 | 0.996 | |
| e0 / e0 | 0.5 | 0.999 |
| Namespace | Name | Value |
|---|---|---|
| e0 / e0, e0e0, e0e2 | 0.27637 | |
| e0 / e0, e0e0, e0e2 | -0.0020901 | |
| e0 / e0, e0e0, e0e2 | 8.125E-6 | |
| e0 / e0, e0e0, e0e2 | -1.4116E-8 | |
| e0 / e0, e0e0, e0e2 | 9.3701E-12 | |
| e0 / e0, e0e0, e0e2 | 0.1058 | |
| e0 / e0, e0e0, e0e2 | -3.6223E-4 | |
| e0 / e0, e0e0, e0e2 | 9.379E-7 | |
| e0 / e0, e0e0, e0e2 | 0.0 | |
| e0 / e0, e0e0, e0e2 | 7.1926E-6 | |
| e0 / e0, e0e0, e0e2 | 298.15 | |
| e0 / e0, e0e0, e0e2 | 298.15 | |
| e0 / e0, e0e0, e0e2 | -241.82 | |
| e0 / e0, e0e0, e0e2 | -200.94 | |
| e0 / e0, e0e0, e0e2 | 61.037 | |
| e0 / e0, e0e0, e0e2 | -7206.7 | |
| e0 / e0, e0e0, e0e2 | -7.1385 | |
| e0 / e0, e0e0, e0e2 | 4.046E-6 | |
| e0 / e0, e0e0, e0e2 | 2.0 | |
| e0 / e0, e0e0, e0e2 | 70.255 | |
| e0 / e0, e0e0, e0e2 | -6876.0 | |
| e0 / e0, e0e0, e0e2 | -8.7078 | |
| e0 / e0, e0e0, e0e2 | 7.1926E-6 | |
| e0 / e0, e0e0, e0e2 | 2.0 | |
| e0 / e0, e0e2 | 52.053 | |
| e0 / e0, e0e2 | 0.3199 | |
| e0 / e0, e0e2 | 0.0 | |
| e0 / e0, e0e2 | 0.0 | |
| e0 / e0, e0e2 | 0.0 | |
| e0 / e0, e0e2 | 52.39 | |
| e0 / e0, e0e2 | 0.3682 | |
| e0 / e0, e0e2 | 0.0 | |
| e0 / e0, e0e2 | 0.0 | |
| e0 / e0, e0e2 | 0.0 | |
| e0 / e0, e0e2 | 647.35 | |
| e0 / e0, e0e2 | 512.64 |
