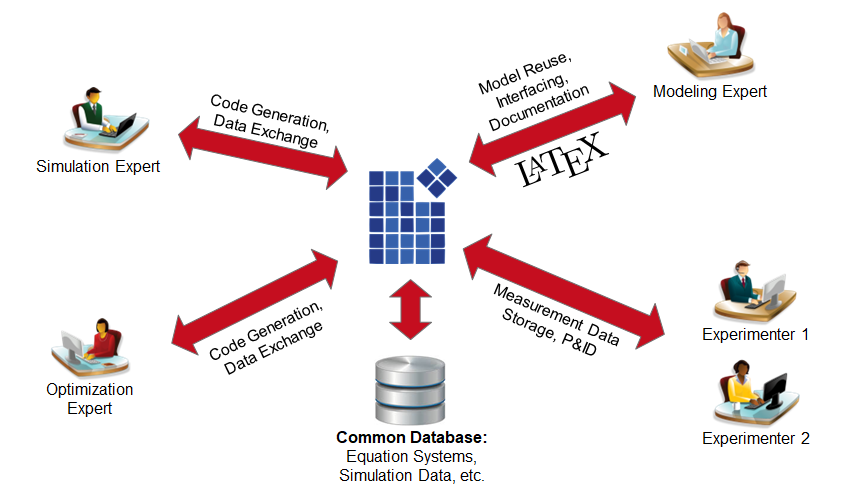
MOSAICmodeling …
- is a free, web-based environment for modeling, simulation, and optimization in process systems engineering;
- uses a LaTeX-style entry method to narrow the gap between documentation and computational description;
- allows the formulation of algebraic as well as ordinary and partial differential equations, which can the be combined to whole equation systems;
- combines several state-of-the-art techniques to support cooperation between different software infrastructures;
- provides code generation for the most common numeric environments, e.g., AMPL, GAMS, gPROMS, MATLAB, Python, and JULIA.
The software offers two main advantages over using various tools for individual tasks (see Figure 1):
- Conventionally, there is a visual and conceptional gap between the documentation and the realization using a particular programming language. In MOSAICmodeling, you receive an easily readable representation of your model, which can then be exported to a program code of your preferred programming language;
- If you try to solve the same problem in several environments, it takes a long time to write and debug each model for each modeling environment. In MOSAICmodeling, you model once, but simulate in whatever software you prefer.