Use of Optimizations I – MINLP Example

On this page

This tutorial explains how a simple process synthesis problem can be set up and solved. This synthesis problem results in an mixed-integer nonlinear programming problem.

Synthesis problem

The synthesis problem contains two options (process I and II) to produce B from A. These processes vary in their fixed and variable costs. In addition, there is the option to simply purchase B directly. Whatever the source of B is, all streams are mixed in a mixer (streams 2, 4, and 5). In the final step, any B is converted to C via process III.

Figure 1: Superstructure for process synthesis example.

Model description

This example is governed by the following equations:

$\begin{align*}&F_{s=2,c} = F_{s=1,c} + R_c^\mathrm{I} \quad \wedge \quad R_c^\mathrm{I} = \nu_c^\mathrm{I} r^\mathrm{I} \ln \left( 1 + F_{s=1,c=1} \right) \\[2ex]&F_{s=4,c} = F_{s=3,c} + R_c^\mathrm{II} \quad \wedge \quad R_c^\mathrm{II} = \nu_c^\mathrm{II} r^\mathrm{II} \ln \left( 1 + F_{s=3,c=1} \right) \\[2ex]&F_{s=7,c} = F_{s=6,c} + R_c^\mathrm{III} \quad \wedge \quad R_c^\mathrm{III} = \nu_c^\mathrm{III} r^\mathrm{III} F_{s=6,c=2} \\[2ex]&F_{s=6,c} = F_{s=2,c} + F_{s=4,c} + F_{s=5,c}\end{align*}$

The first part of each equation is the component balance for the three processes. The second part determines the conversion in each process. Therein, $\nu$ is the stoichiometric coefficient and $r$ is a conversion coefficient. The conversion always depends on the educt feed to the respective process. Finally, there is a component balance for the mixer.

In addition, there are logical / structural constraints:

$\begin{align*}&y^\mathrm{I} + y^\mathrm{II} = c_{i=1} \quad \wedge \quad c_{i=1} \leq 1 \\[2ex]&F_{s=2,c=2} - y^\mathrm{I} F_{s=2,c=2}^\mathrm{max} = c_{i=2} \quad \wedge \quad c_{i=2} \leq 0 \\[2ex]&F_{s=4,c=2} - y^\mathrm{II} F_{s=4,c=2}^\mathrm{max} = c_{i=3} \quad \wedge \quad c_{i=3} \leq 0 \\[2ex]&F_{s=7,c=3} - y^\mathrm{III} F_{s=7,c=3}^\mathrm{max} = c_{i=4} \quad \wedge \quad c_{i=4} \leq 0\end{align*}$

The first constraint ensures that either process I or process II is used, but not both. The other three constraints ensure that the produced product in processes I, II, and III is below the maximum capacity of each process. The processes are activated by the binary decision variables $y^\mathrm{I}$ , $y^\mathrm{II}$ , and $y^\mathrm{III}$ .

Last but not least, the objective function must be formulated. The synthesized process shall be the most cost-efficient option:

$\begin{equation*}\Phi = C^{I,fix} \cdot y^{I} + C^{II,fix} \cdot y^{II} + C^{III,fix} \cdot y^{III}+ C^{I,var}\cdot F_{s=2,c=2} + C^{II,var} \cdot F_{s=4,c=2} + C^{III,var} \cdot F_{s=7,c=3}+ C^{var}_{c=1} \cdot (F_{s=1,c=1}+F_{s=3,c=1}) + C^{var}_{c=2} \cdot F_{s=5,c=2} - C^{var}_{c=3} \cdot F_{s=7,c=3}\end{equation*}$

Hence, the objective function is the sum of fix and variable costs of all processes. The variable costs are only associated with the product stream in this simple example. The last terms represent the costs for educts that must be paid for streams 1, 3, and 5. The objective function is reduced by the income generated by selling the product in stream 7. The binary variables activate these terms in the cost function.

Modeling Workflow

Notation of equation system

For the notation of the equation, we need to set up all base names, superscripts, and indices that appear in the equations, i.e.

Base names

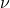$\nu$ , stoichiometric coefficient
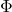$\Phi$ , objective function value
$c$ , constraint dummy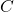
$C$ , cost in EURO
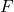$F$ , mass flow in t/h
$r$ , conversion coefficient
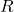$R$ , conversion in t/h
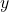$y$ , binary decision variable

Superscripts

fix, fixed cost
I, process I
II, process II
III, process III
max, maximum
var, variable cost

Indices

$c$ , component index 1..NC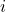
$i$ , constraint index 1..NI
$s$ , stream index 1..NS

The resulting notation has ID 182686.

Equations

Next, we can define the equations of the model. Therefore, we open the equation editor, load the notation we just created, and enter the equations as stated above in the model description. The formulated equations are available with the IDs 182688 to 182698 (11 equations). The objective function has ID 182700.

Equation system

Now we are able to construct our equation system:

Go to “Equation System” and load the notation for the equations
Add the eleven constraints and the objective function to your system in the Connected Elements tab
Save your equation system

This equation system is available with ID 182699.

Simulation workflow

Your model is now complete and you can move on to the “Simulation” section of MOSAICmodeling.

Enter a suitable description
Select the tab Equation System and load the system created in the previous steps. Assign the maximum values for the available indices (NC = 3, NI = 4, NS = 7) and click on Confirm Index Data
Select the tab Specifications. In the list ALL VARIABLES, you will find the variables as defined in your model notation.
Classify the variables as design variables and iteration values, respectively, by selecting the category from the dropdown menu in the Type column.

The simulation will be specified and initialized with the values given in Table 1. After having assigned the initial guesses and the parameter values, you can save the variable specification and then the simulation. The simulation is available in MOSAICmodeling with ID 182704. The respective variable specification that may serve as initialization for the optimization has ID 182705. The solution for both iteration variables and both cases is also given in Table 1. In this case, the solution is equal to the initial guesses, which basically shows that the system is well initialized for optimization.

Name	Description	Value / Initial guess	Solution
$\nu_{c=1}^\mathrm{I}$	Stoichiometric coefficient of component 1 in process I	-1
$\nu_{c=2}^\mathrm{I}$	Stoichiometric coefficient of component 2 in process I	1
$\nu_{c=3}^\mathrm{I}$	Stoichiometric coefficient of component 3 in process I	0
$\nu_{c=1}^\mathrm{II}$	Stoichiometric coefficient of component 1 in process II	-1
$\nu_{c=2}^\mathrm{II}$	Stoichiometric coefficient of component 2 in process II	1
$\nu_{c=3}^\mathrm{II}$	Stoichiometric coefficient of component 3 in process II	0
$\nu_{c=1}^\mathrm{III}$	Stoichiometric coefficient of component 1 in process III	0
$\nu_{c=2}^\mathrm{III}$	Stoichiometric coefficient of component 2 in process III	-1
$\nu_{c=3}^\mathrm{III}$	Stoichiometric coefficient of component 3 in process III	1
$C^\mathrm{I, fix}$	Fix costs of process I in €/h	1000
$C^\mathrm{II, fix}$	Fix costs of process II in €/h	1500
$C^\mathrm{III, fix}$	Fix costs of process III in €/h	3500
$C^\mathrm{I, var}$	Variable costs of process I in €/t	1000
$C^\mathrm{II, var}$	Variable costs of process II in €/t	1200
$C^\mathrm{III, var}$	Variable costs of process III in €/t	2000
$C_{c=1}^\mathrm{var}$	Costs for component 1	1800
$C_{c=2}^\mathrm{var}$	Costs for component 2	7000
$C_{c=3}^\mathrm{var}$	Selling price for component 3	13000
$F_{s=1,c=1}$	Feed of component 1 in stream 1 in t/h	0
$F_{s=3,c=1}$	Feed of component 1 in stream 3 in t/h	0
$F_{s=5,c=1}$	Feed of component 1 in stream 5 in t/h	0
$F_{s=1,c=2}$	Feed of component 2 in stream 1 in t/h	0
$F_{s=3,c=2}$	Feed of component 2 in stream 3 in t/h	0
$F_{s=5,c=2}$	Feed of component 2 in stream 5 in t/h	2
$F_{s=1,c=3}$	Feed of component 3 in stream 1 in t/h	0
$F_{s=3,c=3}$	Feed of component 3 in stream 3 in t/h	0
$F_{s=5,c=3}$	Feed of component 3 in stream 5 in t/h	0
$F_{s=2,c=2}^\mathrm{max}$	Maximum capacity of process I in t/h	4
$F_{s=4,c=2}^\mathrm{max}$	Maximum capacity of process II in t/h	5
$F_{s=7,c=2}^\mathrm{max}$	Maximum capacity of process III in t/h	2
$r^\mathrm{I}$	Conversion factor of process I	1
$r^\mathrm{II}$	Conversion factor of process II	1.2
$r^\mathrm{III}$	Conversion factor of process III	0.9
$y^\mathrm{I}$	Binary decision variable for process I	0
$y^\mathrm{II}$	Binary decision variable for process II	0
$y^\mathrm{III}$	Binary decision variable for process III	1
$F_{s=2,c=1}$	Component flow of component 1 in stream 2	0	0
$F_{s=4,c=1}$	Component flow of component 1 in stream 4	0	0
$F_{s=6,c=1}$	Component flow of component 1 in stream 6	0	0
$F_{s=7,c=1}$	Component flow of component 1 in stream 7	0	0
$F_{s=2,c=2}$	Component flow of component 2 in stream 2	0	0
$F_{s=4,c=2}$	Component flow of component 2 in stream 4	0	0
$F_{s=6,c=2}$	Component flow of component 2 in stream 6	2	2
$F_{s=7,c=2}$	Component flow of component 2 in stream 7	0.2	0.2
$F_{s=2,c=3}$	Component flow of component 3 in stream 2	0	0
$F_{s=4,c=3}$	Component flow of component 3 in stream 4	0	0
$F_{s=6,c=3}$	Component flow of component 3 in stream 6	0	0
$F_{s=7,c=3}$	Component flow of component 3 in stream 7	1.8	1.8
$R_{c=1}^\mathrm{I}$	Conversion rate of component 1 in process I	0	0
$R_{c=2}^\mathrm{I}$	Conversion rate of component 2 in process I	0	0
$R_{c=3}^\mathrm{I}$	Conversion rate of component 3 in process I	0	0
$R_{c=1}^\mathrm{II}$	Conversion rate of component 1 in process II	0	0
$R_{c=2}^\mathrm{II}$	Conversion rate of component 2 in process II	0	0
$R_{c=3}^\mathrm{II}$	Conversion rate of component 3 in process II	0	0
$R_{c=1}^\mathrm{III}$	Conversion rate of component 1 in process III	0	0
$R_{c=2}^\mathrm{III}$	Conversion rate of component 2 in process III	-1.8	-1.8
$R_{c=3}^\mathrm{III}$	Conversion rate of component 3 in process III	1.8	1.8
$c_{i=1}$	Dummy variable 1	0	0
$c_{i=2}$	Dummy variable 2	0	0
$c_{i=3}$	Dummy variable 3	0	0
$c_{i=4}$	Dummy variable 4	-0.2	-0.2
$\Phi$	Objective function value	-2300	-2300

Table 1: Overview of design values and initial guesses.

Optimization workflow

Now that the system is well initialized, move to the “Optimization” section in MOSAICmodeling and go to the Specification tab.

Constraints

Go to the Constraints tab and load your simulation from the previous step. Make sure that all eleven constraints and the objective function are loaded successfully.

Variable specification

Go to the Variable specification. If you saved the simulation after you saved the variable specification, the variable specification from the simulation should be loaded in the optimization as well.

Start by assigning 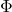$\Phi$ as objective value.
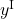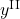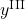Then assign the variables in Table 2 as optimization values and set the given lower and upper bounds. If a value is missing, there is no bound to consider and you can set an arbitrarily high or small value. In addition, define $y^\mathrm{I}$ , $y^\mathrm{II}$ , and $y^\mathrm{III}$ as integer.
You can now save the variable specification – either by overwriting the one from your simulation or by creating a new one. The resulting variable specification with the updated type classifications and variable bounds has ID 182706.
Save the optimization (ID of optimization with this example: 182707).

Name	Lower bound	Upper bound	Integer?
$F_{s=1,c=1}$	0
$F_{s=3,c=1}$	0
$F_{s=5,c=2}$	0
$c_{i=1}$		1
$c_{i=2}$		0
$c_{i=3}$		0
$c_{i=4}$		0
$y^\mathrm{I}$	0	1	Yes
$y^\mathrm{II}$	0	1	Yes
$y^\mathrm{III}$	0	1	Yes

Table 2: Variable bounds for the optimization.

Code generation and solution

Go to the Code Generation & Execution tab. This tab offers two possibilities:

Code generation for use on a local machine
Code generation and execution on the NEOS server

We take the second option by opening the Code Generation & Execution on NEOS Server tab. First, you need to click on Accept & Connect at the bottom to accept the terms of use.

Go to the Submit tab and take the following steps:

Select Mixed Integer Nonlinearly Constrained Optimization as Category
Select BONMIN as Solver (you need to actually click on it before Language can be selected)
Select AMPL as Language
Click on Generate Code & Submit

Go to the tab History. If the job does not appear in your history, click on “Refresh”. Once the status is “Done”, you can click on the job and scroll down to the results.

You can copy these results and re-import them into MOSAICmodeling by doing the following:

In the Specification tab, go to the Variable Specification tab and click on “Import Values”
Paste the results into this window and select AMPL as Language Specification (at the top). You can click on “Test Import” to see whether the variables are correctly recognized.
Click on Import. This updates all variable values in your variable specification.
If you want to, you can save this new variable specification with another name, e.g., “Results”

Results

The results obtained with BONMIN are given below in Table 3. Values that were numerically zero are shown as 0 for clarity. The results indicate that the best option under the current constraint is using process II and buying additional B, which is then used to produce C. The variable specification containing the results has ID 182729.

Name	Description	Value / Initial guess	Solution
$\nu_{c=1}^\mathrm{I}$	Stoichiometric coefficient of component 1 in process I	-1
$\nu_{c=2}^\mathrm{I}$	Stoichiometric coefficient of component 2 in process I	1
$\nu_{c=3}^\mathrm{I}$	Stoichiometric coefficient of component 3 in process I	0
$\nu_{c=1}^\mathrm{II}$	Stoichiometric coefficient of component 1 in process II	-1
$\nu_{c=2}^\mathrm{II}$	Stoichiometric coefficient of component 2 in process II	1
$\nu_{c=3}^\mathrm{II}$	Stoichiometric coefficient of component 3 in process II	0
$\nu_{c=1}^\mathrm{III}$	Stoichiometric coefficient of component 1 in process III	0
$\nu_{c=2}^\mathrm{III}$	Stoichiometric coefficient of component 2 in process III	-1
$\nu_{c=3}^\mathrm{III}$	Stoichiometric coefficient of component 3 in process III	1
$C^\mathrm{I, fix}$	Fix costs of process I in €/h	1000
$C^\mathrm{II, fix}$	Fix costs of process II in €/h	1500
$C^\mathrm{III, fix}$	Fix costs of process III in €/h	3500
$C^\mathrm{I, var}$	Variable costs of process I in €/t	1000
$C^\mathrm{II, var}$	Variable costs of process II in €/t	1200
$C^\mathrm{III, var}$	Variable costs of process III in €/t	2000
$C_{c=1}^\mathrm{var}$	Costs for component 1	1800
$C_{c=2}^\mathrm{var}$	Costs for component 2	7000
$C_{c=3}^\mathrm{var}$	Selling price for component 3	13000
$F_{s=1,c=1}$	Feed of component 1 in stream 1 in t/h	0	0
$F_{s=3,c=1}$	Feed of component 1 in stream 3 in t/h	0	2.87
$F_{s=5,c=1}$	Feed of component 1 in stream 5 in t/h	0	0.6
$F_{s=1,c=2}$	Feed of component 2 in stream 1 in t/h	0
$F_{s=3,c=2}$	Feed of component 2 in stream 3 in t/h	0
$F_{s=5,c=2}$	Feed of component 2 in stream 5 in t/h	2
$F_{s=1,c=3}$	Feed of component 3 in stream 1 in t/h	0
$F_{s=3,c=3}$	Feed of component 3 in stream 3 in t/h	0
$F_{s=5,c=3}$	Feed of component 3 in stream 5 in t/h	0
$F_{s=2,c=2}^\mathrm{max}$	Maximum capacity of process I in t/h	4
$F_{s=4,c=2}^\mathrm{max}$	Maximum capacity of process II in t/h	5
$F_{s=7,c=2}^\mathrm{max}$	Maximum capacity of process III in t/h	2
$r^\mathrm{I}$	Conversion factor of process I	1
$r^\mathrm{II}$	Conversion factor of process II	1.2
$r^\mathrm{III}$	Conversion factor of process III	0.9
$y^\mathrm{I}$	Binary decision variable for process I	0	0
$y^\mathrm{II}$	Binary decision variable for process II	0	1
$y^\mathrm{III}$	Binary decision variable for process III	1	1
$F_{s=2,c=1}$	Component flow of component 1 in stream 2	0	0
$F_{s=4,c=1}$	Component flow of component 1 in stream 4	0	1.24
$F_{s=6,c=1}$	Component flow of component 1 in stream 6	0	1.24
$F_{s=7,c=1}$	Component flow of component 1 in stream 7	0	1.24
$F_{s=2,c=2}$	Component flow of component 2 in stream 2	0	0
$F_{s=4,c=2}$	Component flow of component 2 in stream 4	0	1.62
$F_{s=6,c=2}$	Component flow of component 2 in stream 6	2	2.2
$F_{s=7,c=2}$	Component flow of component 2 in stream 7	0.2	0.22
$F_{s=2,c=3}$	Component flow of component 3 in stream 2	0	0
$F_{s=4,c=3}$	Component flow of component 3 in stream 4	0	0
$F_{s=6,c=3}$	Component flow of component 3 in stream 6	0	0
$F_{s=7,c=3}$	Component flow of component 3 in stream 7	1.8	2
$R_{c=1}^\mathrm{I}$	Conversion rate of component 1 in process I	0	0
$R_{c=2}^\mathrm{I}$	Conversion rate of component 2 in process I	0	0
$R_{c=3}^\mathrm{I}$	Conversion rate of component 3 in process I	0	0
$R_{c=1}^\mathrm{II}$	Conversion rate of component 1 in process II	0	-1.62
$R_{c=2}^\mathrm{II}$	Conversion rate of component 2 in process II	0	1.62
$R_{c=3}^\mathrm{II}$	Conversion rate of component 3 in process II	0	0
$R_{c=1}^\mathrm{III}$	Conversion rate of component 1 in process III	0	0
$R_{c=2}^\mathrm{III}$	Conversion rate of component 2 in process III	-1.8	-2
$R_{c=3}^\mathrm{III}$	Conversion rate of component 3 in process III	1.8	2
$c_{i=1}$	Dummy variable 1	0	1
$c_{i=2}$	Dummy variable 2	0	0
$c_{i=3}$	Dummy variable 3	0	-3.38
$c_{i=4}$	Dummy variable 4	-0.2	0
$\Phi$	Objective function value	-2300	-5697.1

Table 3: Initialization and results of the optimization.