In this example, the connected equations have different notations. They have only one common (generic) variable ![]() . Using the naming policy encapsulate makes it possible to specify only the translation of this common variable while ensuring that all other variables are not matched by accident.
. Using the naming policy encapsulate makes it possible to specify only the translation of this common variable while ensuring that all other variables are not matched by accident.
Model description
As in example II for connectors, the equation system reads
![Rendered by QuickLaTeX.com \begin{align*} z_{k=1} + A \cdot z_{k=2} = B \\[2ex] C \cdot z_{k=2}^{2} = -D + z_{k=1}. \end{align*}](https://mosaic-modeling.de/wp-content/ql-cache/quicklatex.com-c2a7f05b1147eebc6a91c13dbc63db8a_l3.png)
Workflow
Notation
We use the same super notation as in example II. This notation has ID 182746.
Equations
Likewise, the same equations as in example II for connectors with IDs 182732 and 182733 can be used.
Connectors
Now we again need to create two connectors. Go to the Connector tab and proceed as follows:
- Add a helpful description for the connector
- Activate the tab Edit Matching. You see two sections: one for the Sub Notation and one for the Super Notation. Both sections contain a field to import the notation
- In the section for the Sub Notation, press the Import button and select the notation of the colleague, then confirm. Alternatively, you can select Import Notation from Connected Element and select the equation of the colleague. This automatically adds all variables used in this equation
- Add the new super notation as Super Notation. As there is no analogous equation available, you need to select Import Notation directly
- Generate the missing variables for the Sub Notation and the Super Notation, i.e.,
- Sub Notation:
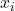
- Super Notation:
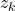
- Sub Notation:
- Select the analogous variables and click on Match to achieve the following matching:
- Make sure by clicking on the pair
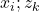 to check whether the Index Matching was successful. The Sub index
to check whether the Index Matching was successful. The Sub index 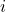 should have been matched with the Super index
should have been matched with the Super index 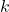
- Save the connector
- Repeat these steps for a new connector that connects the user notation and the new super notation. The variables in this case are:
- Sub Notation:
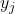
- Super Notation:
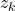
- Sub Notation:
- The resultung match must be:
- Verify the correct setup of the connector and save it
The connectors are available with IDs 182756 and 182757. Figure 1 illustrates how both equations are combined to one equation system.
 Figure 1: Visualization of the variable naming when using the connector. Note: this figure must be updated to match the variables and names used in this example.
Figure 1: Visualization of the variable naming when using the connector. Note: this figure must be updated to match the variables and names used in this example.
Equation system
To construct the equation system, go to the Equation System tab and take the following steps.
- Load the user equation from example I with the connector user notation
 super notation
super notation - Load the colleague’s equation from example I with the connector colleague notation
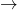 super notation
super notation - Save the equation system
The equation system has ID 182758.
Evaluation / Simulation
Go to the “Simulation” section and do the following:
- Load your equation system in the tab Equation System
- Set the maximum Value NK to 2 in the tab Indexing
- Go to the tab Specifications; you will notice that the variables from the original notations, i.e.,
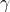 and
and 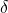 as well as
as well as  and
and 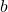 , are part of the problem, but they have received their own namespace e0e0 and e0e1, respectively
, are part of the problem, but they have received their own namespace e0e0 and e0e1, respectively - Assign the variables
 ,
, 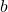 ,
, 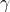 , and
, and 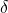 as design values
as design values - Assign the variables
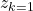 and
and 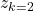 as iteration values
as iteration values
Initialization and results
To initialize and specify the model, take the following steps:
- Initialize this example with the design values and initial guesses given in the previous examples
- Save the variable specification
- Save the simulation
- Go to the Evaluation tab and generate the code for your preferred environment
- Solve the system using the generated code
This simulation is available with ID 182759 with variable specification 182760. The solution will be the same as in the previous examples. To conclude this set of examples, we note that encapsulate can be very powerful to quickly connect various equations or equation systems as long as you do not mind the additional namespaces.
