Use of Basic Elements I – Algebraic Equation System

On this page

This first example shall be used to familiarize new users with the basic workflow of MOSAICmodeling. Hence, the solved problem is not very complex or hard to set up.

Model description

The model consists of two equations:

$0 = a \left( 1 - x \right) \\[2ex] 0 = b \left( y - x^2 \right).$

Therein, $a$ and $b$ are design values, i.e., variables we know the values of. On the other hand, $x$ and $y$ are unknown quantities. We want to determine the values of these two variables given the model above and the values we will assign to $a$ and $b$ .

Model workflow

We will now go through the model workflow within MOSAICmodeling. Of course, the software was developed to solve problems in chemical engineering, but it is virtually applicable to any mathematical problem.

Notation

We always begin by setting up a notation. A notation is a specification of which variables may appear in our model. Further explanations can be found in the documentation of the notation. A variable can consist of base names, superscripts and subscripts, and indices. As you can see, our model variables only consist of base names. Therefore, perform the following steps to set up your notation:

Go to the Notation tab in the “Model” section
Add a description of your notation, e.g., “This is the notation of my first MOSAIC example”
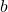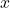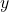Add the base names $a$ , $b$ , $x$ , and $y$ by clicking on “+ Name” at the bottom, entering these names, adding a description of the variable (e.g., “parameter” or “variable”), and confirming it
Once you have added all four variables, click on “Save” at the top of the editor and save your notation at a suitable location in your folder structure

The notation of this example has ID 182858.

Equations

Go to the Equation tab. Now, we will formulate the two model equations. Proceed as follows:

Load the notation you just created
Add an informative description of the current equation, e.g., “This is the first model equation”
Type the first model equation in LaTeX style into the window MosaicTex: 0 = a \cdot (1 – x)
Save the equation at a suitable location in your folder structure
Click on “New” at the top of the editor and repeat the steps 1 and 2
Enter the second model equation: 0 = b \cdot (y – (x)^{2}). Note that you need curly brackets around exponents (and superscripts) and round brackets to specify that the base x has an exponent of 2
Save this second equation as well

The two equations are available in MOSAICmodeling with the IDs 182859 and 182860.

Equation system

Now, we will combine our equations to an equation system. To this end, go to the Equation System tab and carry on as described below:

Load your notation from above
Add a suitable description
Go to the tab Connected Elements and click on “+ EQU/EQS” at the bottom of the editor
In the opening popup window, select your two equations and confirm (you can also add them one-by-one). They will then appear in the overview of connected elements
Save your equation system

The equation system has ID 182861 within MOSAICmodeling.

With this last step, the modeling part within MOSAICmodeling is completed. The remaining workflow will discuss the problem specification and explain the code generation and solution.

Simulation workflow

Start by going to the “Simulation” section of MOSAICmodeling.

Equation system

Go to the tab Equation System and select your newly saved equation system from above.

Indexing

Proceed to the tab Indexing. If you had defined any indices in your notation that appear in your model equations, you could specify the maximum value of this index. For example, if you had defined $c$ as component index, you could now set 2 as maximum values for two components in your system.

Specification

Go to the tab Specifications and then select the tab Variables. Proceed as follows:

Add a helpful description of the simulation
In the specification window, you can see all possible variable classifications. Select ALL VARIABLES at the top. You should now see the four variables that are part of your model
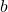Change the entry in the column Type for $a$ and $b$ to Design Value. This means that they are treated as constants during the solution
Change the type classification of the other two variables to iteration value. Your degree of freedom should now be zero
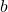Assign the values given in Table 1 to the four variables. Note that the values of $a$ and $b$ do not really matter, of course due to the mathematical structure of the problem; but this example is only intended to illustrate the basic workflow
Save your variable specification by clicking on the “Save” button above the calculation of the degrees of freedom
Save your simulation by clicking on “Save” at the top of the editor

The simulation is available with ID 182862. The associated variable specification has ID 182863.

Table 1: Overview of design values, initial guesses, and the solution.

Name	Description	Value / Initial guess	Solution
$a$	Parameter 1	50
$b$	Parameter 2	100
$x$	Variable 1	0	1.0
$y$	Variable 2	0	1.0

Evaluation

Finally, we want to determine the solution of our model:

Go to the Evaluation tab, then go to the Code Generation tab
Select your preferred language specification, e.g., Matlab
Click on Generate Code
Go to the tab View Code and copy the code into your respective modeling environment, e.g., Matlab
Execute the code and analyze the solution

You can find the solution of the model in Table 1 as well.