Use of Optimizations II – Dynamic Optimization via Single Shooting

On this page

Model description

This example shows how to solve a dynamic optimization problem with single shooting via MOSAICmodeling. The case study focuses on a CSTR for which two inputs must be optimally chosen so that the integral of component 1 over a time horizon of one hour is maximized. The example is governed by the following equations:

$\begin{align*}&\frac{\mathrm{d}c_c}{\mathrm{d}t} = \frac{F}{V} \cdot (c_c^\mathrm{in} - c_c) + \sum_{r=1}^{NR}\nu_{c,r} \cdot k_r \cdot c_{c=r} \cdot \exp(-\frac{E_r}{R \cdot T}) \\[2ex]&\frac{\mathrm{d}T}{\mathrm{d}t} = \frac{F}{V} \cdot (T^\mathrm{in} - T) + \sum_{r=1}^{NR} k_r \cdot c_{c=r} \cdot \exp(-\frac{E_r}{R \cdot T}) \cdot \frac{-\Delta h_{\mathrm{R},r}}{\rho \cdot cp} - \frac{UA}{\rho \cdot cp \cdot V} \cdot (T - T_\mathrm{jacket}) \\[2ex]&\frac{\mathrm{d}c_{c=1}^\mathrm{integral}}{\mathrm{d}t} = c_{c=1} \\[2ex]&ineq = T - T^\mathrm{max} \\[2ex]&f = - c_{c=1}^\mathrm{integral}.\end{align*}$

The first equation is the generic component balance. The second equation is the energy balance. The third equation determines the integral of the concentration of component 1 numerically. The fourth equation represents an inequality constraint that specifies the upper bound of the reactor temperature. Finally, the last equation calculates the objective value for the optimization. This is the negative integral as we want to minimize the function later on.

Modeling Workflow

Notation of equation system

For the notation of the equation, we need to set up all base names, superscripts, and indices that appear in the equations, i.e.

Base names

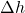$\Delta h$ , enthalpy difference in kJ/mol
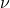$\nu$ , stoichiometric coefficient
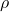$\rho$ , density in kg/m³
$c$ , molar concentration in mol/m³
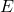$E$ , activation energy in J/mol
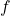$f$ , objective
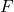$F$ , volume flow in m³/s
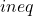$ineq$ , inequality slack variable in K
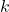$k$ , pre-exponential factor for kinetics in 1/s
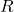$R$ , universal gas constant in J/mol/K
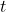$t$ , time in s
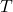$T$ , temperature in K
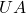$UA$ , product of overall heat transfer coefficient and jacket are in kW/K
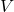$V$ , volume in m³

Superscripts

in, inlet
integral, integral over time horizon
max, maximum

Subscripts

jacket, reactor jacket
R, reaction

Indices

$c$ , component index 1..NC
$r$ , reaction index 1..NR

The resulting notation has ID 185805.

Equations

Next, we can define the equations of the model. Therefore, we open the equation editor, load the notation we just created, and enter the equations as stated above in the model description. The formulated equations are available with the IDs 185806, 185807, 185819, 185811, and 185812 (5 equations).

Equation system

Now we are able to construct our equation system:

Go to “Equation System” and load the notation for the equations
Add the eleven constraints and the objective function to your system in the Connected Elements tab
Save your equation system

This equation system is available with ID 185808.

Simulation workflow

Your model is now complete and you can move on to the “Simulation” section of MOSAICmodeling.

Enter a suitable description
Select the tab Equation System and load the system created in the previous steps. Assign the maximum values for the available indices (NC = 3, NR = 2) and click on Confirm Index Data
Select the tab Specifications. In the list ALL VARIABLES, you will find the variables as defined in your model notation.
Classify the variables as design variables and iteration values, respectively, by selecting the category from the dropdown menu in the Type column.

The simulation will be specified and initialized with the values given in Table 1. After having assigned the initial guesses and the parameter values, you can save the variable specification and then the simulation. The simulation is available in MOSAICmodeling with ID 185809. The respective variable specification that may serve as initialization for the optimization has ID 185810.

Name	Description	Value / Initial guess / Initial condition
$\Delta h_{\mathrm{R},r=1}$	Enthalpy of reaction for reaction 1	45000.0
$\Delta h_{\mathrm{R},r=2}$	Enthalpy of reaction for reaction 2	-55000.0
$\nu_{c=1,r=1}$	Stoichiometric coefficient of component 1 for reaction 1	-1
$\nu_{c=1,r=2}$	Stoichiometric coefficient of component 1 for reaction 2	1
$\nu_{c=2,r=1}$	Stoichiometric coefficient of component 2 for reaction 1	0
$\nu_{c=2,r=2}$	Stoichiometric coefficient of component 2 for reaction 2	-1
$\nu_{c=3,r=1}$	Stoichiometric coefficient of component 2 for reaction 1	1
$\nu_{c=3,r=2}$	Stoichiometric coefficient of component 3 for reaction 2	0
$\rho$	Density	800.0
$E_{r=1}$	Activation energy of reaction 1	69000.0
$E_{r=2}$	Activation energy of reaction 2	72000.0
$F$	Volume flow of feed	6.5E-4
$R$	Universal gas constant	8.3144598
$T^\mathrm{in}$	Inlet temperature	333.0
$T^\mathrm{max}$	Maximum temperature	350.0
$T_\mathrm{jacket}$	Temperature of jacket	333.0
$UA$	Cooling characteristic	1.4
$V$	Volume	1.0
$c_{c=1}^\mathrm{in}$	Inlet concentration of component 1	5.0
$c_{c=2}^\mathrm{in}$	Inlet concentration of component 2	20.0
$c_{c=3}^\mathrm{in}$	Inlet concentration of component 3	3.0
$cp$	Heat capacity	3.5
$k_{r=1}$	Pre-exponential factor of reaction 1	5.0E6
$k_{r=2}$	Pre-exponential factor of reaction 2	1.0E7
$T$	Initial condition for temperature	333.0
$c_{c=1}$	Initial condition for concentration of component 1	8.0
$c_{c=2}$	Initial condition for concentration of component 2	20.0
$c_{c=3}$	Initial condition for concentration of component 3	0.0
$c_{c=1}^\mathrm{integral}$	Initial condition for integral of concentration of component 1	0.0
$ineq$	Initial guess for slack variable	-17.0
$f$	Initial guess for objective	0.0

Table 1: Overview of design values, initial conditions, and initial guesses.

Optimization workflow

Now move to the “Optimization” section in MOSAICmodeling and go to the Specification tab.

Constraints

Go to the Constraints tab and load your simulation from the previous step. Make sure that all constraints and the objective function are loaded successfully.

Variable specification

Go to the Variable specification. If you saved the simulation after you saved the variable specification, the variable specification from the simulation should be loaded in the optimization as well.

Start by assigning 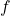$f$ as objective value.
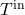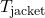Then assign $T^\mathrm{in}$ and $T_\mathrm{jacket}$ as optimization values and set their lower and upper bounds to 273 and 373, respectively
Set an upper bound of 0 for $ineq$
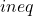
You can now save the variable specification – either by overwriting the one from your simulation or by creating a new one.
Save the optimization

The resulting variable specification with the updated type classifications and variable bounds has ID 185817. The optimization has ID 186816.

Code generation and execution

Go to the tab Code Generation & Execution and take a look at the Status window: It should read 1 variable selected for minimization and 2 variables selected for optimization. Load the user-defined language specificator with ID 185804, which is created in the example Use of User-defined Language Specifications II – Parameter Estimation with Single Shooting and click on Generate Code. Copy the export to Matlab and solve this optimization problem sequentially. Note that the algorithm ‘SQP’ is chosen as preference because this was the only algorithm that was able to solve this problem. The default algorithm ‘Interior-point’ might be able to solve the problem if the algorithm’s parameters are modified. With the default options, it terminates with an infeasible solution. The optimal solution for the two controls $T^\mathrm{in}$ and $T_\mathrm{jacket}$ are 327 K and 328 K, respectively. However, the solution depends on the initial guesses for the decisions as the only constraint for the maximum temperature is active and the reactor temperature can either be reduced by a lower inlet temperature or a lower cooling temperature.

Note that the used UDLS is still fairly simple as only one control setpoint is allowed over the full time horizon of one hour. Of course, this could be further refined.