Use of Optimizations III – NLP Example

On this page

This tutorial explains how a nonlinear programming problem can be set up and solved.

Model description

This example minimizes the objective function $\Phi$ , subject to an equality constraint and an inequality constraint as well as the bounds of the variables:

$\min_{x_i} \Phi = x_{i=1} \cdot x_{i=4} \cdot (x_{i=1} + x_{i=2} + x_{i=3}) + x_{i=3} \\[3ex] \mathrm{s.\,t.\,} x_{i=1}^2 + x_{i=2}^2 + x_{i=3}^2 + x_{i=4}^2 = 40, \\[2ex] \phantom{\mathrm{s.\,t.\,}} x_{i=1} \cdot x_{i=2} \cdot x_{i=3} \cdot x_{i=4} \geq 25, \\[2ex] \phantom{\mathrm{s.\,t.\,}} 1 \leq x_i \leq 5.$

The example is known as Hock & Schittkowski Problem #71.

Modeling Workflow

Notation of equation system

For the notation of the equation, we need to set up all base names, superscripts, and indices that appear in the equations, i.e.

Base names

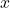$x$ , variable
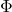$\Phi$ , objective function value

Indices

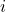$i$ , variable index 1..NI

The resulting notation has ID 185950.

Equations

Next, we can define the equations of the model. Therefore, we open the equation editor, load the notation we just created, and enter the equations as stated above in the model description. Note that inequalities can be expressed via the LaTeX commands \leq and \geq

The formulated equations are available with the IDs 185951, 185952, and 185953.

Equation system

Now we are able to construct our equation system:

Go to “Equation System” and load the notation for the equations
Add the eleven constraints and the objective function to your system in the Connected Elements tab
Save your equation system

This equation system is available with ID 185954.

Simulation workflow

Your model is now complete and you can move on to the “Simulation” section of MOSAICmodeling.

Enter a suitable description
Select the tab Equation System and load the system created in the previous steps. Set the maximum value of the index 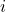$i$ to 4 and click on Confirm Index Data
Select the tab Specifications. In the list ALL VARIABLES, you will find the variables as defined in your model notation.
Arbitrarily classify three variables as design variables and the remaining two as iteration values, respectively, by selecting the category from the dropdown menu in the Type column.

After having assigned the initial guesses and the parameter values, you can save the variable specification and then the simulation. The simulation is available in MOSAICmodeling with ID 185955. The respective variable specification that may serve as initialization for the optimization has ID 185956. The solution for both iteration variables and both cases is also given in Table 1. In this case, the solution is equal to the initial guesses, which basically shows that the system is well initialized for optimization.

Optimization workflow

Now go to the “Optimization” section of MOSAICmodeling and load the simulation. Then, go to the Variable Specification tab and assign $\Phi$ as OBJECTIVE_VAR and $x_i$ as OPTIMIZATION_VAR. One of the $x_i$ is arbitrarily assigned as ITERATION_VALUE. Assign the bounds given in the model description to the four variables and solve the optimization problem by exporting it to your local environment or by solving it via the NEOS server (description in example “Use of Optimizations I – MINLP Example”). Both initial guesses and solution are given in Table 1.

The optimization has ID 185958 and the associated variable specification has ID 185959.

\Phi — Table 1: Initialization and results of the optimization.

x_{i=1} — Table 1: Initialization and results of the optimization.

Name	Description	Initial guess	Solution
$\Phi$	Objective	0.0	17.014
$x_{i=1}$	Variable 1	1.0	1.0
$x_{i=2}$	Variable 2	5.0	4.74
$x_{i=3}$	Variable 3	5.0	3.82
$x_{i=4}$	Variable 4	1.0	1.38