Use of Optimization IV – MILP Example

On this page

This tutorial explains how a simple mixed-integer linear programming problem can be set up and solved.

Model description

This example is governed by the following equations:

$\begin{align*} &\min_{x_i} \Phi = -20 x_{i=1} - 6 x_{i=2} - 8 x_{i=3}\\[3ex] \mathrm{s.\,t.\quad} &0.8 x_{i=1} + 0.2 x_{i=2} + 0.3 x_{i=3} \leq 20, \\[2ex] \phantom{\mathrm{s.\,t.\,}} &0.4 x_{i=1} + 0.3 x_{i=2} \leq 10, \\[2ex] \phantom{\mathrm{s.\,t.\,}} &0.2 x_{i=1} + 0.1 x_{i=3} \leq 5, \\[2ex] \phantom{\mathrm{s.\,t.\,}} &0 \leq x_i \leq \infty, \\[2ex] \phantom{\mathrm{s.\,t.\,}} &x_i \in \mathbb{N}. \end{align*}$

The example is taken from here.

Modeling Workflow

Notation of equation system

For the notation of the equation, we need to set up all base names, superscripts, and indices that appear in the equations, i.e.

Base names

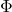$\Phi$ , objective function value
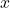$x$ , variable

Indices

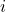$i$ , variable index 1..NI

The resulting notation has ID 186252.

Equations

Next, we can define the equations of the model. Therefore, we open the equation editor, load the notation we just created, and enter the equations as stated above in the model description. The formulated equations are available with the IDs 186253 to 186255, and 186256. The objective function has ID 186260.

Equation system

Now we are able to construct our equation system:

Go to “Equation System” and load the notation for the equations
Add the eleven constraints and the objective function to your system in the Connected Elements tab
Save your equation system

This equation system is available with ID 186261.

Simulation workflow

Your model is now complete and you can move on to the “Simulation” section of MOSAICmodeling.

Enter a suitable description
Select the tab Equation System and load the system created in the previous steps. Assign the maximum values for NI = 3 and click on Confirm Index Data
Select the tab Specifications. In the list ALL VARIABLES, you will find the variables as defined in your model notation.
Classify the variables as design variables and iteration values, respectively, by selecting the category from the dropdown menu in the Type column.

You can save the variable specification and then the simulation. The simulation is available in MOSAICmodeling with ID 186262. The respective variable specification that may serve as initialization for the optimization has ID 186263.

Optimization workflow

Go to the “Optimization” section of MOSAICmodeling and load the simulation from above. Go to the Variable Specification, select the $x_i$ as OPTIMIZATION_VAR and $\Phi$ as OBJECTIVE_VAR. Check the field Integer for the $x_i$ .

Now, we would like to export the model and solve it. However, many MILP solvers simply expect matrices and vectors for lower and upper bounds of constraints. MOSAICmodeling is not capable of providing that – even with UDLS capabilities – because the software does not understand structures such as matrices and vectors. Instead, the constraints are exported as is. If the user adheres to a strict index policy, e.g., by naming all coefficients in the constraints according to a fixed scheme containing constraint and variable index. However, additional steps would be necessary to automatically obtain the matrix structure that MILP solvers in Matlab or Python expect.

Due to these reasons, we solve our models with GAMS or AMPL and do not continue with setting up a UDLS for these software packages. Instead, we go to the tab Code Generation & Execution and connect to the NEOS server (tab Code Generation & Execution on NEOS Server). Here, the user must accept the Terms of Use, select Mixed Integer Linear Programming as Category, choose a solver from the list, and select the preferred language. Then, click on Generate Code & Submit and inspect the results in the tab History. The following solution is obtained with CBC and AMPL:

$x_{i=1} = 0$
$x_{i=2} = 31$
$x_{i=3} = 46$
$\Phi = -554$

The optimization is available with ID 186264, the adapted variable specification with ID 186265