This tutorial demonstrates how to use connectors for a dynamic system. This could, for example, be necessary because you want to use a dynamic sub-model of a colleague. Here, we want to use the sub-system of a PI controller. If we did not use a connector for the time variable, MOSAICmodeling would issue a warning because we had two different time variables. MOSAICmodeling would interpret this as a partial differential equation, which can currently not be solved.
Model description
This example is based on the article by Asprey and Macchietto (2002), DOI: 10.1016/S0959-1524(01)00020-8. It features two differential equations representing the concentrations of the components as well as an expression for the reaction rate:
![Rendered by QuickLaTeX.com \begin{align*} \frac{\mathrm{d}x^\mathrm{B}}{\mathrm{d}t} = \left( r - u - \theta_{i=4} \right) x^\mathrm{B} \\[2ex]\frac{\mathrm{d}x^\mathrm{S}}{\mathrm{d}t} = - \frac{r x^\mathrm{B}}{\theta_{i=3}} + u \left( x_\mathrm{F}^\mathrm{B} - x^\mathrm{S} \right) \\[2ex]r = \frac{\theta_{i=1} x^\mathrm{S}}{\theta_{i=2} + x^\mathrm{S}}. \end{align*}](https://mosaic-modeling.de/wp-content/ql-cache/quicklatex.com-5aaea1c733604287482e28e2d0c268da_l3.png)
In addition, we want to add a PI controller to this system. This PI controller consists of the following generic equations, which have to be matched to the system above via a connector:
![Rendered by QuickLaTeX.com \begin{align*} u = K_\mathrm{P} e_\mathrm{P} + K_\mathrm{I} e_\mathrm{I} + u^\mathrm{set} \\[2ex]e_\mathrm{P} = y^\mathrm{set} - y \\[2ex]\frac{\mathrm{d}e_\mathrm{I}}{\mathrm{d}t} = e_\mathrm{P}. \end{align*}](https://mosaic-modeling.de/wp-content/ql-cache/quicklatex.com-aee879336157ec9070f28ddc0ad7d9e3_l3.png)
Note that the ![]() in the PI equations is the same
in the PI equations is the same ![]() in the model equations above.
in the model equations above.
Modeling workflow
In the following, we show the workflow for setting up the model with both open loop and closed loop. We start by defining the notation for this example. Then, we define the notation of the controller equations.
Notation of model
Set up a notation with the following base names and indices:
Base names
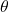 , parameter in various units
, parameter in various units , reaction rate in 1/h
, reaction rate in 1/h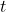 , time in h
, time in h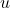 , dilution factor in 1/h
, dilution factor in 1/h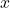 , molar concentration in g/L
, molar concentration in g/L
Superscripts
- B, biomass
- S, substate
- SP, setpoint
Subscripts
- F, feed
Indices
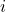 , parameter index 1…NI
, parameter index 1…NI
The resulting notation has ID 2323.
Notation of controller
Base names
 , control deviation
, control deviation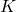 , gain factor
, gain factor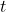 , time in h
, time in h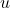 , manipulated variable
, manipulated variable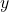 , control variable
, control variable
Superscripts
- set, setpoint
Subscripts
- I, integral part
- P, proportional part
The resulting notation has ID 186460.
Equations of the model
Go to the Equation tab and perform the following steps:
- Load the model notation set up above
- Enter the model equations
The model equations have IDs 2324, 2325, and 2326.
Equations of the controller
Go to the Equation tab and perform the following steps:
- Load the controller notation set up above
- Enter the model equations
The model equations have IDs 186459, 186461, and 186462.
Connectors
To connect these two equation systems, we will need a connector. One could suggest to simply use the naming policy integrate as this would create the same namespace for all variables and there would only be one variable ![]() . However, the two models could also use completely different variable names for time, e.g.,
. However, the two models could also use completely different variable names for time, e.g., ![]() and
and ![]() in a more generic case. In this case here, we also need to match the controlled variables:
in a more generic case. In this case here, we also need to match the controlled variables: ![]() in the generic model of the PI controller and
in the generic model of the PI controller and ![]() in the model equations. For this purpose, go to the Connector tab and do the following:
in the model equations. For this purpose, go to the Connector tab and do the following:
- Add a helpful description for the connector
- Activate the tab Edit Matching and select the controller equation as Sub Notation and the model notation of this example as Super Notation
- Generate the missing variables for the Sub Notation and the Super Notation, i.e.,
- Sub Notation:
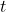 ,
, 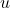 ,
, 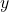 ,
, 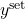
- Super Notation:
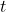 ,
, 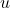 ,
, 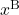 ,
, 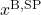
- Sub Notation:
- Select the analogous variables and click on Match to achieve the following matching:
- Save the connector
The connector has ID 2351.
Equation system for open loop
To construct this equation systems, go to the Equation System tab and take the following steps.
- Load the model notation and add a reasonable description
- Click on “Add EQU/EQS” and add the three model equations
- Make sure that the Naming policy is integrate
- Save the equation system
Equation system for PI controller
To construct this equation systems, go to the Equation System tab and take the following steps.
- Load the controller notation and add a reasonable description
- Click on “Add EQU/EQS” and add the three controller equations
- Make sure that the Naming policy is integrate
- Save the equation system
Equation system for closed loop
We now combine the two previous equation systems:
- Load the model notation and add a reasonable description
- Click on “Add EQU/EQS” and add the equation system of the model
- Make sure that the Naming policy is integrate
- Click again on “Add EQU/EQS” and add the equation system of the controller; select encapsulate as naming policy and select the connector from above; then confirm
- Save the equation system
The naming policy encapsulate is chosen arbitrarily in this case and the policy integrate would also work. In general, we recommend encapsulate, though, as you avoid undesired matches between variables in your individual sub-models.
The equation system for open loop is available with ID 2334, the equation system of the controller has ID 186463, and the equation system for closed loop has ID 2352.
Simulation workflow
Equation system and Indexing
Equation system for open loop
Go to the “Simulation” section and do the following:
- Load your equation system for the open loop in the tab Equation System
- Set the maximum value NI to 4 in the tab Indexing
Equation system for closed loop
Go to the “Simulation” section and do the following:
- Load your equation system for the closed loop in the tab Equation System
- Set the maximum value NI to 4 in the tab Indexing
Initialization and results
Equation system for open loop
Go to the tab Specifications and open the Variables tab. To initialize and specify the model, take the following steps:
- Initialize this example with the design values and initial guesses given in Table 1
- Save the variable specification
- Save the simulation
- Go to the Evaluation tab and generate the code for your preferred environment
- Solve the system using the generated code
This simulation is available with ID 2335 with variable specification 2334.
Equation system for closed loop
Go to the tab Specifications and open the Variables tab. To initialize and specify the model, take the following steps:
- Initialize this example with the design values and initial guesses given in Table 2
- Save the variable specification
- Save the simulation
- Go to the Evaluation tab and generate the code for your preferred environment
- Solve the system using the generated code
This simulation is available with ID 2354 with variable specification 2353.
When you simulate the system with open loop and closed loop, you can observe the impact of the controller on the model performance.
| Name | Description | Value / Initial condition / Initial guess |
|---|---|---|
| Parameter 1 | 0.325 | |
| Parameter 2 | 0.267 | |
| Parameter 3 | 0.559 | |
| Parameter 4 | 0.055 | |
| Reaction rate | 0.01 | |
| Time, independent variable | 0.0 | |
| Control | 0.2 | |
| Mass concentration of biomass | 1.0 | |
| Mass concentration of substrate | 0.01 | |
| Mass concentration of substrate in feed | 30.0 |
| Name | Description | Value / Initial condition / Initial guess |
|---|---|---|
| Parameter 1 | 0.325 | |
| Parameter 2 | 0.267 | |
| Parameter 3 | 0.559 | |
| Parameter 4 | 0.055 | |
| Gain factor of integral controller | 0.001 | |
| Gain factor of proportional controller | 0.001 | |
| Control deviation for integral controller | 0.0 | |
| Control deviation for proportional controller | 0.0 | |
| Reaction rate | 0.01 | |
| Time, independent variable | 0.0 | |
| Control | 0.2 | |
| Feedforward control value | 0.0 | |
| Mass concentration of biomass | 1.0 | |
| Controller setpoint | 12.0 | |
| Mass concentration of substrate | 0.01 | |
| Mass concentration of substrate in feed | 30.0 |
Use of functions
If you prefer to formulate an ODE system in which certain algebraic variables are calculated via functions, you can do so. For this example, the reaction rate was also formulated as function. In this case, the parameters 1 and 2 must be added to a parameter list (ID: 189115). This parameter list is then used in the function because non-generic indices cannot appear in the function body (ID: 189116). Finally, the function replaces the algebraic equation for the reaction rate in a new equation system (ID: 189114). This equation system is used in a new simulation with ID 189119, using the variable specification with ID 189117 and the parameter specification with ID 189118. The values are the same as given in Table 1. The results with be the same, but the system is now used with an ODE solver instead of a DAE solver.
