Use of Transformations I – Orthogonal Collocation on Finite Elements

This example demonstrates how to automatically transform an existing ODE or DAE system into an algebraic equation system using a specified discretization scheme, in this case orthogonal collocation on finite elements.

Model description

As application, we choose the ODE system of the example Use of Basic Elements III – Orthogonal Collocation on Finite Elements.

Workflow

We now demonstrate the workflow. The first step is the definition of a notation for the discretization scheme.

Notation of the discretization

Set up a notation with the following base names and indices:

Base names
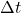  • \Delta t, length of finite element
  • a, collocation coefficient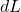
  • dL, Derivative of lagrange basis polynomial
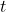  • t, time
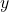  • y, state variable
Indices
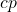  • cp, index of collocation points 1…NCP
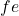  • fe, index of collocation points 1…NFE
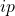  • ip, index of interpolation polynomials 1…NIP

The resulting notation has ID 185836.

Equations and equation system for discretization scheme

For orthogonal collocation, two equations are required:

\frac{\mathrm{d}y}{\mathrm{d}t} = \frac{1}{\Delta t_{fe}} \sum_{ip=0}^{NIP} y_{cp=ip,fe} \cdot dL_{ip,cp} \\[2ex] y_{cp=NCP,fe-1} = y_{cp=0,fe}.

The first equation is the discretization, the second ensures continuity between finite elements. Enter these equations by taking the following steps:

  1. Load the notation of the discretization scheme
  2. Enter the first equation
  3. Save the equation
  4. Enter and save the second equation
  5. Go to the tab Equation system, add these two equations, and save the equation system

The equations have IDs 185833 and 185834. The equation system has ID 185835.

Transformation

Now, we define the transformation. To this end, go to the Transformation tab and take the following steps:

  1. Add a helpful description for the transformation
  2. Add the equation system with the discretization scheme as EQS (Discretization) and the notation of the model you want to transform (here: ID 8480) as Super Notation
    Attention: the super notation must include three free indices that can be matched in the next step. If these do not exist, add them to the notation before you proceed
  3. Go to the tab Variable Matching and add 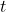t for both the Discretization and the Super Notation. Match them
  4. In the bottom right corner, click on “Add discretization index” and write 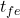t_{fe}. The index 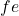fe appears at the bottom right corner for the Sub Notation. Add the index 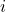i (can be different for any other used-defined notation) for the Super Notation
  5. Go to the tab Index Matching and match the indices as follows (left: Discretization, right: Super Notation):
    • cp \leftrightarrow c
    • fe \leftrightarrow i
    • ip \leftrightarrow j
  6. Go to the tab Variable Predermination. MOSAICmodeling can sometimes have issues with recognizing the correct variables to be discretized. Therefore, add z as variable and set it as state variable
  7. Save the transformation

The transformation is available with ID 185836.

Discretized equation system

To discretize the original equation system, go to the Equation System tab and take the following steps.

  1. Load the notation of the original ODE system (ID 8480)
  2. Click on “Add EQU/EQS” and select the equation system of the original ODE system (ID 8482), but do not confirm to close this popup window
  3. Make sure that the Naming policy is integrate
  4. Turn on the option Apply transformation(s) and select the saved transformation
  5. Confirm
  6. Save the equation system.
  7. If you go to the tab Preview and click on “Update Preview”, you should now see the automatically discretized ODE system

The equation system has ID 185837. You could now go to the “Simulation” section, load this equation system, specify the indices, and use the variable specification from the example Use of Basic Elements III – Orthogonal Collocation on Finite Elements. The solution should be the same.